피보나치 수열 (Fibonacci)

수학에서 피보나치 수는 첫째 및 둘째 항이 주어졌을 때 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열을 말한다. 예시로 1 1 2 3 5 로 표현할 수 있다. 이는 다음과 같은 점화식으로 정의된다.

F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2) (n >= 2)

오늘은 프로젝트 오일러의 Project 2 문제로 피보나치 수열을 풀어보려고 한다.

피보나치(Fibonacci) 수열의 각 항은 바로 앞의 항 두 개를 더한 것입니다. 1과 2로 시작하는 경우 이 수열은 아래와 같습니다.
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
4백만 이하의 짝수 값을 갖는 모든 피보나치 항을 더하면 얼마가 됩니까?

위 문제의 해결 아이디어는 다음과 같다. 피보나치 수열을 4백만까지 반복하고 짝수 항인 경우 누적합에 더하는 방법이다. 피보나치 수열 풀이의 대표적인 방법인 반복문, 재귀, DP 방식을 각각 활용하여 풀이법을 작성해보았다. 전체 코드를 먼저 보고 상세 내용을 보자.

package euler;

import java.util.HashMap;
import java.util.Map;

// 1과 2로 시작하는 피보나치 수열에서 4백만 이하이면서 짝수인 항의 합
public class P2 {

    // 1. 반복문 활용
    private static int loop(int limit, int first, int second) {
        int sum = 0;
        while (second <= limit) {
            if (second % 2 == 0) {
                sum += second;
            }
            int next = first + second;
            first = second;
            second = next;
        }
        return sum;
    }

    // 2. 재귀 활용
    private static int fib(int n) {
        if (n == 0) return 1;
        if (n == 1) return 2;
        return fib(n - 1) + fib(n - 2);
    }

    private static int recursion(int limit) {
        int sum = 0;
        int n = 0;
        int current;

        while (true) {
            current = fib(n);
            if (current > limit) break;
            if (current % 2 == 0) {
                sum += current;
            }
            n++;
        }
        return sum;
    }


    // 3. DP 활용 (재귀 + 메모이제이션)
    private static Map<Integer, Integer> memo = new HashMap<>();

    private static int topDownFib(int n) {
        if (n == 0) return 1;
        if (n == 1) return 2;
        if (memo.containsKey(n)) return memo.get(n);
        int result = topDownFib(n - 1) + topDownFib(n - 2);
        memo.put(n, result);
        return result;
    }

    private static int topDowndp(int limit) {
        int sum = 0;
        int n = 0;
        int current;

        while (true) {
            current = topDownFib(n);
            if (current > limit) break;
            if (current % 2 == 0) {
                sum += current;
            }
            n++;
        }
        return sum;
    }

    public static void main(String[] args) {

        int limit = 4000000;
        int first = 1;
        int second = 2;

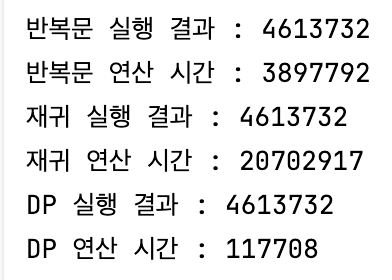
        // 3 가지 방법의 연산 시간을 알아보자.
        Long loopStartTime = System.nanoTime();
        System.out.println("반복문 실행 결과 : " + loop(limit, first, second));
        Long loopEndTime = System.nanoTime();
        System.out.println("반복문 연산 시간 : " + (loopEndTime - loopStartTime));

        Long recursionStartTime = System.nanoTime();
        System.out.println("재귀 실행 결과 : " + recursion(limit));
        Long recursionEndTime = System.nanoTime();
        System.out.println("재귀 연산 시간 : " + (recursionEndTime - recursionStartTime));

        Long dpStartTime = System.nanoTime();
        System.out.println("DP 실행 결과 : " + topDowndp(limit));
        Long dpEndTime = System.nanoTime();
        System.out.println("DP 연산 시간 : " + (dpEndTime - dpStartTime));

    }

}

1️⃣ 반복문 활용

가장 기본적이고 쉽게 생각할 수 있는 방법이다. 단순히 연산을 반복하면서 짝수를 찾아 누적합에 더한다. 반복문의 시간 복잡도는 O(n) 이다. 각 피보나치 항은 한 번씩만 계산되므로 연산 시간이 선형적으로 증가한다.

private static int loop(int limit, int first, int second) {
    int sum = 0;
    while (second <= limit) {
        if (second % 2 == 0) {
            sum += second;
        }
        int next = first + second;
        first = second;
        second = next;
    }
    return sum;
}

2️⃣ 재귀 활용

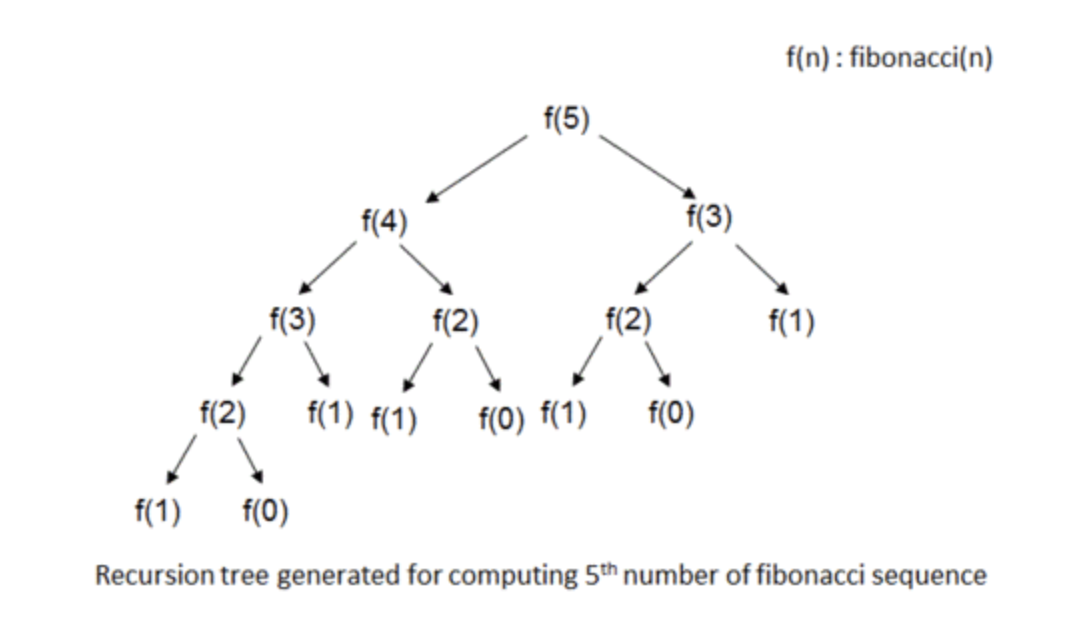
fib(n) 을 반복적으로 호출하여 순수 재귀로 계산한다. 아래 이미지를 보면 fib(5) 로 피보나치 수열의 5번째 항을 계산할 때 재귀 연산이 어떤 식으로 동작하는지 알 수 있다. 동일한 값을 반복해서 재계산 하므로 시간 복잡도는 O(n^2) 이다. 작은 수에서는 괜찮지만 n 이 증가할수록 연산 시간이 기하 급수적으로 느려진다.

private static int fib(int n) {
    if (n == 0) return 1;
    if (n == 1) return 2;
    return fib(n - 1) + fib(n - 2);
}

3️⃣ DP 활용 (top-down)

재귀 방식의 단점을 개선하기 위해 메모이제이션을 활용할 수 있다. 이런 방식을 DP (Dynamic Programming, 동적 계획법) 라고 하는데 큰 문제를 작은 문제로 쪼개서 푸는 방식을 말하며, 한 번 계산한 문제는 다시 계산하지 않도록 하는 알고리즘이다. 그리고 메모이제이션이란 DP 를 구현하는 방법 중 한 종류이다. 재귀 함수로 한 번 구한 문제는 메모리 공간에 저장해두고 같은 식을 호출하면 저장한 결과를 그대로 가져오도록 하는 기법이다. 보통은 Map 을 쓸 것 같은데… 나는 메모 공간을 HashMap 으로 구현했다. LinkedHashMap 을 사용해도 되지만 이번 경우는 피보나치 항이 저장되는 순서는 중요하지 않으므로 HashMap 을 사용했다.

시간 복잡도는 반복문과 동일하게 O(n) 이다.

private static Map<Integer, Integer> memo = new HashMap<>();

private static int topDownFib(int n) {
    if (n == 0) return 1;
    if (n == 1) return 2;
    if (memo.containsKey(n)) return memo.get(n);
    int result = topDownFib(n - 1) + topDownFib(n - 2);
    memo.put(n, result);
    return result;
}

🔍 반복문 방식과 DP 방식의 시간 복잡도가 O(n) 으로 동일한데 n 값이 증가한다면 어떤 방식이 더 유리할까?

반복문과 DP 방식 모두 시간 복잡도는 O(n) 이지만, n 이 커질수록 반복문 방식이 더 유리하다. 여기서는 공간 복잡도를 고려해볼 수 있는데, 반복문의 경우 공간 복잡도가 O(1) 인데 반해 DP 의 경우 공간 복잡도가 O(n) 이다. 반복문은 int 변수 몇 개로 계산을 하고 DP 는 재귀하는 깊이만큼 스택이 쌓이고 Map 이 사용되기 때문에 공간 사용도가 선형적으로 증가하는 것이다.

항목	반복문	DP (재귀+메모이제이션)
시간 복잡도	O(n)	O(n)
공간 복잡도	O(1)	O(n)
함수 호출 오버헤드	없음	있음 (함수 호출 스택 사용)
메모리 사용량	낮음	높음
재귀 깊이 한계	없음	있음 (StackOverFlow 위험)