Q 2015 수들의 합 4
💡 문제 요약 및 분석
정수 N 과 K 가 주어졌을 때, N 개의 정수가 들어가는 배열 A 에서 부분합이 K 가 되는 경우의 수를 출력하면 된다.
💡 알고리즘 설계
🔥 도저히 모르겠어서 답을 보고 풀었다. 시간 안에 풀려면 누적합 배열 + Map 을 활용해야 한다.
입력
- 표준입력 받는 숫자를 누적합한 배열 sum 을 만든다.
연산
부분합 k 를 어떻게 구할 것인가가 관건이었는데, 시간 안에 풀려면 다음과 같은 공식을 생각해냈어야 한다.
sum[j] - sum[i - 1] = k sum[j] - k = sum[i - 1]즉 누적합 배열 sum[j] - K 의 값을 갖는 sum[i - 1] 인덱스가 존재한다면 count 변수에 더하면 된다. 이를 판단하기 위해서는 Map 이 필요하다.
- HashMap 생성하여 기본값으로 map.put(0,1) 넣기. 왜냐하면 sum[j] - K == 0 일 때가 있을 수 있기 때문에 미리 값을 넣어주는 것이다.
- for 문으로 N 까지 반복한다. (최대 200,000번 수행)
- map 에서 sum[i] - K 의 값을 key 로 갖는 값을 찾는데, 없으면 0을, 있으면 value 를 count 에 더한다.
- map.put(sum[i], map.getOrDefault(sum[i],0) + 1) 하여 확인이 끝난 sum[i] 인덱스를 key 로 넣어준다. 이 때 value 는 1을 넣어주는데, 다음 연산에서 해당 key 가 조회되었을 때 count 하기 위함이다.
출력
- count 변수를 출력한다.
💡 코드
import java.io.*;
import java.util.HashMap;
import java.util.Map;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
long K = Long.parseLong(st.nextToken());
long[] sum = new long[N + 1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i < N + 1; i++) {
sum[i] += sum[i - 1] + Long.parseLong(st.nextToken());
}
Map<Long, Long> map = new HashMap<>();
map.put(0L,1L);
long count = 0;
for (int i = 1; i < N + 1; i++) {
count += map.getOrDefault(sum[i] - K, 0L);
map.put(sum[i], map.getOrDefault(sum[i], 0L) + 1);
}
System.out.println(count);
}
}

💡 시간 복잡도, 공간 복잡도
| 시간 복잡도 | 공간 복잡도 |
|---|---|
| O(n) | O(n) |
💡 느낀점 및 기억할 정보
👩🏻💻 부분합 알고리즘
배열의 일부 구간의 합을 빠르게 구할 수 있게 해주는 알고리즘이다. N 개의 원소로 이루어진 배열이 주어졌을 때, 반복문으로 부분 배열의 합을 구하려면 O(n) 걸리는데, 부분합을 이용하면 모든 부분합을 O(1) 에 구할 수 있다.
1️⃣ 1차원 배열 arr 이 주어졌을 때, 일단 각 원소를 누적합한 배열 sum 을 새로 만든다.
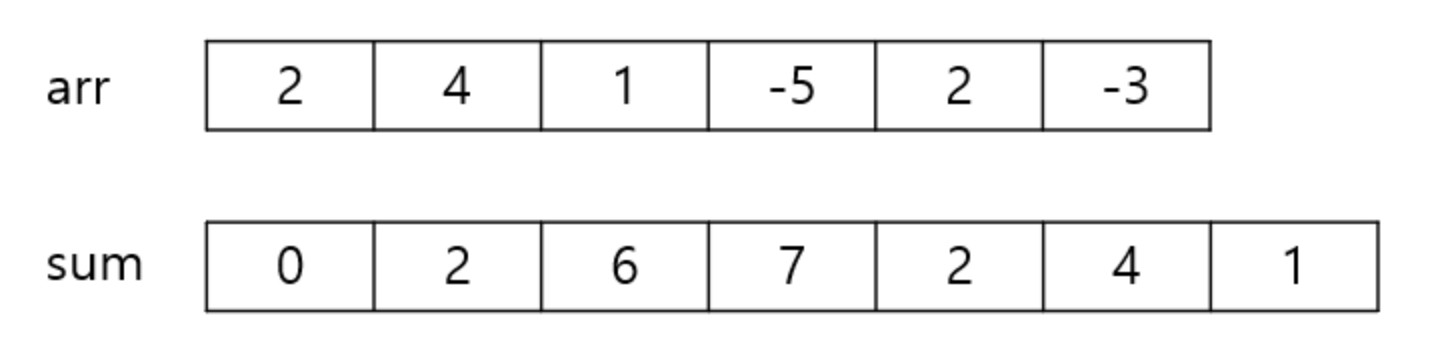
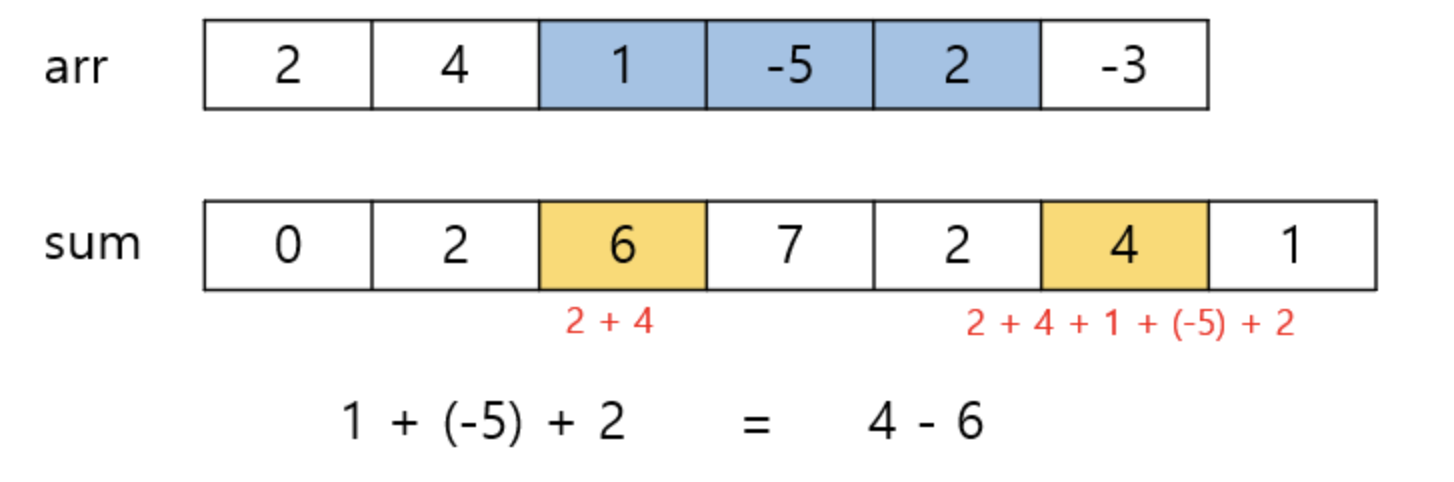
2️⃣ arr 배열의 i항부터 j항까지의 합을 S(i,j) 라고 하자. 이 때 S(i,j) = S(j + 1) - S(i) 가 된다.
📎 참고자료